【DWS】微流變學

Microrheology

微流變學（microrheology），是一種將膠體示蹤粒子（tracer particle）分散置入樣品中當作探針的流變學量測方法，示蹤粒子的半徑大小一般介於0.3至2.0 μm之間，可以自由地融入懸浮液、乳膠或任何有興趣的介質系統當中，示蹤粒子的運動狀況直接反映它們在局部環境中的流變特性，由圖1(a)可以看到，對於完全黏性樣品，示蹤粒子可以在整個系統中自由擴散移動，這樣的結果使示蹤粒子的均方位移（Δr² (τ)）與時間呈線性關係（如圖2(a)紅色線所示）。

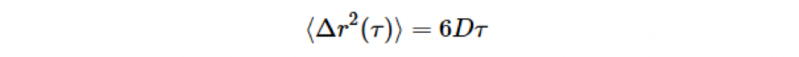
如同標準的史托克斯－愛因斯坦（Stokes-Einstein equation）方程式中，D代表粒子的擴散係數（diffusing coefficient）：

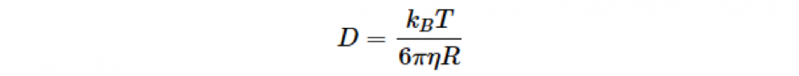
帶入所測得的均方位移（Δr² (τ)）到這幾個方程式中，得到內含示蹤粒子（已知半徑為R）的牛頓溶劑之黏度η（viscosity），然而，若材料中同時包含有彈性的組成分時，均方位移（Δr² (τ)）會呈現更複雜的時間相依性，這使得上述方程式不完全適用。

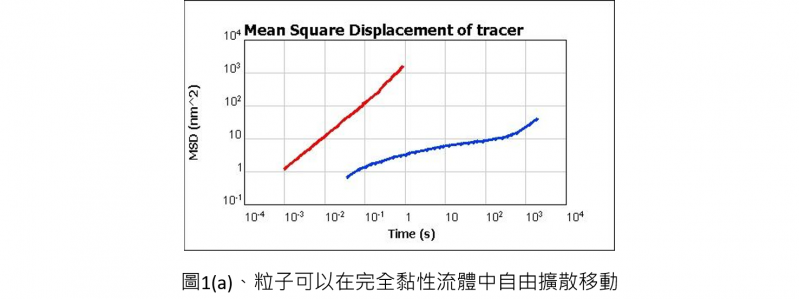
這可以用含聚苯乙烯示踪粒子的明膠溶液的例子來說明。在升高溫度時（例如50℃），明膠溶液為單純的液體，示蹤粒子可自由擴散（如圖1(a)），然而，在低溫下時（例如15℃），明膠形成凝膠，使示蹤粒子陷落在網狀結構中（如圖1(b)）。在布朗運動中，熱能只允許以振動的方式產生局部形變，而振動又與局部環境的剛性有關。示蹤粒子的運動受到限制，使得在均方位移（Δr² (τ)）的關係曲線中呈現高原的現象（如圖2(a)中藍線所示），此時振幅為其相對應的最大位移，這是明膠網狀結構的強度特性。但是，許多材料是複雜的流體，其表現出黏性和彈性這兩種行為，這就是我們所稱的黏彈性材料。他們的反應通常取決於測量時所探測到的長度和時間大小有關。自然體現黏彈性行為的方式可藉由廣義的史托克斯-愛因斯坦關係式來解釋[1]︰

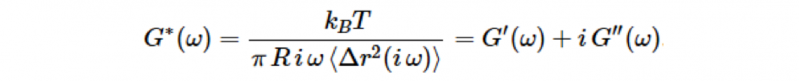
這個方程式允許從量測到的均方位移（Δr² (τ)）計算具頻率相依性的儲存模數G'(ω)和損失模數G''(ω)。在我們明膠溶液的例子中，從微流變學中所得到的G'(ω)和G''(ω)數值如圖2(b)所示，說明一個純流體（pure liquid）在高溫下（以紅虛線表示）損失模數G''(ω)與頻率ω成比例關係，而儲存模數G'(ω)則非常小，以至於超出圖表的範圍。然而，在低溫下（以藍線表示），在某個頻率範圍下，儲存模數G'(ω)佔主導地位，且高於損失模數G''(ω)，只有在非常高頻率以上的時候，兩條曲線會產生交叉，此後損失模數G''(ω)會比儲存模數G'(ω)大。這可以透過凱文－佛伊格特模型（Kelvin-Voigt model）來描述這樣的特性（如圖2(c)），它是由彈簧和緩衝器以並聯方式組成的，彈簧代表明膠網狀結構的彈性，而緩衝器表示黏性阻尼器，以此來形容水分子圍繞在明膠網狀結構的耗散效應（dissipative effect）。

• (a) 紅色代表自由擴散粒子的均方位移，藍色代表陷落粒子的均方位移。

• (b) 紅色代表高溫下的G"(ω)（紅虛線），藍色代表低溫下的G'(ω)（藍線）和G''(ω)（藍虛線）。

• (c) 凱文-佛伊格特模型（Kelvin-Voigt model）由彈簧和緩衝器以並聯方式組成。

大部分的微流變學方法是屬於「被動式（passive）」，換言之，示蹤粒子在樣品中的移動是依靠熱能（kBT），如同布朗運動一樣。只有幾種特殊的方式（例如光鉗、磁性流變學）是屬於「主動式（active）」的，換言之，透過外部的力量，例如能量大於熱能（kBT）的光或磁力，來驅動示蹤粒子的移動。主動式方法的優點是粒子移動的振幅是可以被控制的，因此，能有效量測流變學中線性或非線性的特性。另一方面，被動式微流變學適合在線性黏彈性範圍區間（linear viscoelastic region, LVR）的量測，因為只需要微弱的熱能即可確保示蹤粒子在移動中能產生小的震幅變化。

微流變學進一步可以利用不同的方法來量測示蹤粒子的均方位移（Δr² (τ)），以下三種是最常用的技術︰

粒子追蹤微流變學（Particle tracking microrheology）

利用架設在顯微鏡上的攝影機以及軟體，依序紀錄追蹤粒子的運動軌跡，計算出粒子的均方位移（Δr² (τ)）之後，接著便可得到介質的流變特性，這項技術可以額外得到粒子在非均勻樣品中不同局部區域的運動資訊，這項技術的缺點是，必須費力地調整追蹤參數和處理數據，此外，由於光學顯微鏡的空間解析度的限制，因此只能被用於示蹤粒子可以移動顯著距離的低黏度樣品。

動態光散射法微流變學（DLS microrheology）

利用動態光散射法求得示蹤粒子的均方位移（Δr² (τ)），其空間解析度與顯微鏡法微流變技術差不多，造成動態光散射法微流變技術只能被用於示蹤粒子可以移動顯著距離的低黏度樣品，相較於顯微鏡法微流變技術，其主要的優點在於量測與數據處理上更直接且快速。

擴散波光譜法微流變學（DWS microrheology）

利用擴散波光譜法求得示蹤粒子的均方位移（Δr² (τ)），這樣的探測技術比動態光散射法微流變儀技術及顯微鏡法微法微流變技術需要更多的樣品量，這將使同樣是在一分鐘量測時間內能產生增強統計數據的效果，此外，相較於動態光散射法與顯微鏡法的微流變技術，擴散波光譜法能大幅提高空間解析度，因此，連示蹤粒子運動會被嚴重限制住的高黏度樣品，甚至非各態歷經（non-ergodic）樣品都可以量測。最後，擴散波光譜法微流變技術最重要的特色是，它可以進行高達到10⁷ rad/s（約1 MHz）的頻率的量測，反觀機械式流變儀頻率最大只能達到約10² rad/s（約15 Hz）。

DWS RheoLab II是LS Instruments所生產的擴散波光譜法流變儀，搭配先進的光散射技術，是一台體積小、耐用且多功能的儀器，它與傳統的機械式流變儀不同，將樣品密封在玻璃光析管（Glass Cuvette）中，因此可以延長量測時間，進行樣品穩定度與老化的研究。此外，一般機械式流變儀在量測時，頻率最大只能達到約100 Hz，而且在做多段頻率掃描量測時，經常要花好幾個小時；反觀DWS RheoLabII，由於其搭配「Two-Cell-Echo Technology」專利技術，從0.1Hz到10⁶ Hz進行多段頻率掃描量測，只需短短幾分鐘之內即可得到精確且可靠的儲存模數G'(ω)和損失模數G''(ω)數據結果。

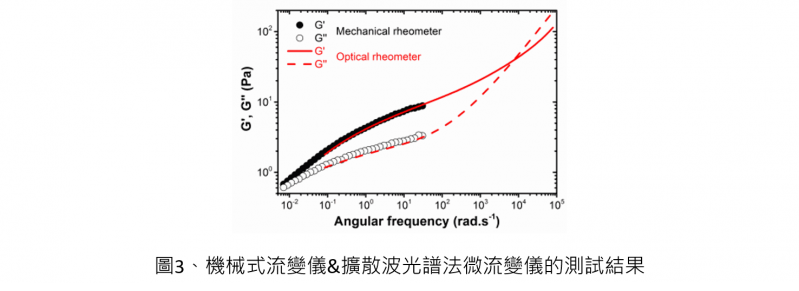
圖3︰機械式流變儀與擴散波光譜法微流變儀RheoLab，在量測0.55%（wt/v）黃原膠溶液（Xanthan）儲存模數G'(ω)和損失模數G''(ω)的比較。在做微流變學的量測時，加入1 %（wt/v）粒徑980 nm的聚苯乙烯粒子（Polystyrene, PS）到黃原膠溶液中，圖中黑色曲線代表利用機械式流變儀測試的結果，紅色曲線代表用擴散波光譜法微流變儀的測試結果，從圖中可以發現，在低頻率區段兩者結果一致，但是，擴散波光譜法微流變儀可以量測到更高頻率區段下的儲存模數G'(ω)和損失模數G''(ω)。

資料來源

• Mason, T. G.; Weitz, D. A. Optical Measurements of Frequency-Dependent Linear Viscoelastic Moduli of Complex Fluids, Physical Review Letters 74, 1250-1253 (1995).
• http://www.lsinstruments.ch/technology/diffusing_wave_spectroscopy_dws/microrheology/

關鍵字詞

• Microrheology︰微流變學。
• Tracer Particle︰示蹤粒子。
• MSD, Mean Square Displacement︰均方位移。
• Stokes-Einstein equation︰史托克斯－愛因斯坦方程式。
• Diffusing Coefficient︰擴散係數。
• η, Viscosity︰黏度。
• Gelatin︰明膠。
• G'(ω), Storage Modulus︰儲存模數。
• G''(ω), Loss Modulus︰損失模數。
• Kelvin-Voigt Model︰凱文-佛伊格特模型。
• Dissipative effect︰耗散效應。
• Optical Tweezer︰光鉗。
• Brownian motion︰布朗運動。
• Amplitude︰振福。
• LVR, Linear Viscoelastic Region︰線性黏彈性範圍區間。
• Particle tracking microrheology︰粒子追蹤微流變學。
• DLS microrheology︰動態光散射法微流變學。
• DWS microrheology︰擴散波光譜法微流變學。
• Spatial Resolution︰空間解析度。
• Xanthan︰黃原膠。