【DWS】擴散波光譜法在乳膠特性上的應用

Emulsions characterized by DWS

前言

擴散波光譜法（Diffusing Wave Spectroscopy，簡稱DWS），是一種功能性強的光散射技術，可以應用在混濁樣品（turbid samples）流變學特性的研究。這個方法是以分析雷射光在樣品內經過多次散射所產生的波動為基礎[1,2]。LS Instruments所生產的DWS RheoLab II是一台耐用且功能性強的儀器，非常適合用於這些特性的檢測。

應用擴散波光譜技術時，需要界定清楚的是，散射物體必須是在樣品之內，它們可以原本就是樣品本身的一部分，或者是有目的的添加，（例如在使用DWS測量上，針對透明樣品需添加示蹤粒子以增加樣品濁度），在這兩種情況下的散射體，被稱為示蹤粒子（tracer particles），並且具理想地單分散性和很高的光學對比度，然而，乳膠（例如化妝水、面霜、或牛奶）中的散射體是液體微滴（liquid droplets），並非固體粒子，微滴在乳膠中的尺寸分佈通常顯示相當的多分散性（polydispersity）。

此應用實例的目的是為了證明，當採用擴散波光譜技術時，乳膠微滴（emulsion droplets）仍然可充當天然的示蹤粒子，用以探測乳膠的流變特性，在此方法中，我們將黃原膠（xanthan）加入含油的水溶液中，形成黃原膠的體積分率為20 vol.%的乳膠，其中黃原膠是當作黏度修飾劑（viscosity modifier），以此為系統模型進行測試，另外，我們也將擴散波光譜微流變儀所量測到的乳膠黏彈特性，與傳統機械式流變儀的結果進行比較。

樣品製備

連續相的製備，是將0.55 wt.%的黃原膠（xanthan）以及0.3 wt.%的殺菌劑Cosmocil一起溶於蒸餾水中。為了避免對熱敏感[3]，將此溶液加熱3 小時至85℃，接著攪拌48小時。乳膠的製備，是取164克上述的連續相，加熱至50℃後，加入2.1克的乳化劑Tween 80，在均質化的過程中加入34克的杏仁油(almond oil, 密度︰0.91 g/mL)，接著繼續均質12分鐘。在準備完樣品之後，所有的測試均在25℃下進行，且於14天內完成。

乳膠的特性

首先將乳膠透過共軛焦顯微鏡觀察，可以獲得微滴的尺寸。圖一顯示乳膠用脂溶性螢光染劑（lipophilic Nile red）染色的影像。油微滴分散的很好，而且完全被拘束在黃原膠連續相的本體中，插圖顯示相對應微滴大小的分佈情況。

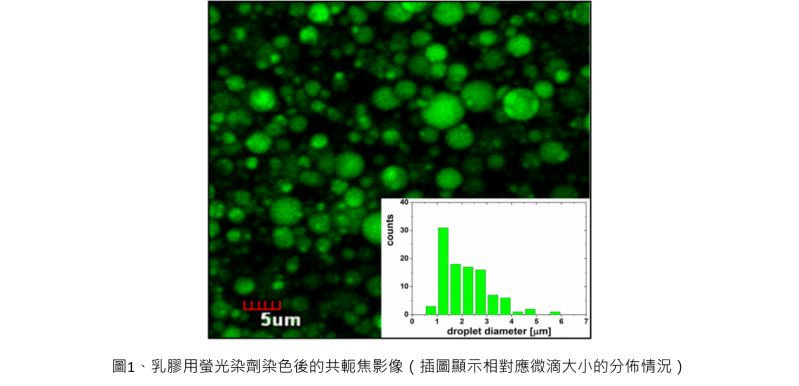
乳膠用螢光染劑染色後的共軛焦影像。插圖顯示相對應微滴大小的分佈情況。

使用內徑2 mm的光析管，採用前向散射（transmission）模式進行擴散波光譜技術的乳膠測試，用1wt.%，粒徑980nm溶於水中的聚苯乙烯粒子進行校正，測得的運輸平均自由徑l*數值為226 μm。對應圖一插圖中分佈最多的微滴尺寸，因此我們選擇使用粒徑為1.2μm的示蹤粒子。機械式流變儀使用的是Malvern Bohlin Gemini流變儀，配備噴砂圓錐形狀（60 mm，2°）的夾具與溶劑回收系統，儲存模數G'和損失模數G''的量測條件為利用振盪模式（oscillation mode），0.1固定振幅，（是因為在1Hz下進行振幅掃描測試時，發現振幅0.1可在其線性的黏彈性範圍內），圖二比較由擴散波光譜法微流變儀與機械式流變儀測得的G'和G''數值，在頻率重疊的範圍，兩者的數據顯得相當一致。

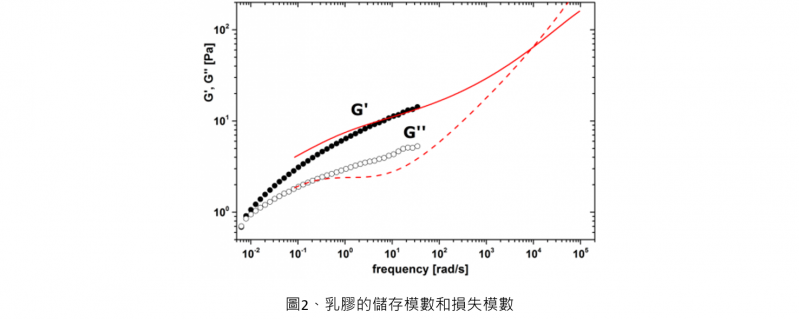
乳膠的儲存模數（以實心記號，及實線表示）和損失模數（以空心記號，及虛線表示）。紅色「線」表示擴散波光譜法微流變儀的數據，黑色「記號」表示機械式流變儀的數據。

連續相

所製備的乳膠中，其分散相佔的體積百分比並不高，因此，流變學特性主要是由連續相所決定的。我們測試模型系統的連續相，是由已知流變性質的0.55wt.%黃原膠所構成的凝膠[3,4]。我們分別用擴散波光譜法微流變儀與機械式流變儀進行連續相的測定。機械式流變儀測定時，我們使用和測試乳膠時所用的參數一樣。用擴散波光譜法微流變儀測定連續相時，如同之前的方式，將粒徑980 nm溶於水中的聚苯乙烯粒子添加到0.58wt.%的黃原膠溶液中，最後得到的混合物連續相中含有1wt.%聚苯乙烯粒子，0.3 wt.%的Cosmocil以及0.55 wt.%的黃原膠。因此，用聚苯乙烯粒子探測相對於乳膠中連續相的環境。在擴散波光譜法中所用的光析管內徑為2mm，採用前向散射模式，用1wt.%，粒徑980nm溶於水中的聚苯乙烯粒子進行校正，測得乳膠的運輸平均自由徑l*數值為398 μm。

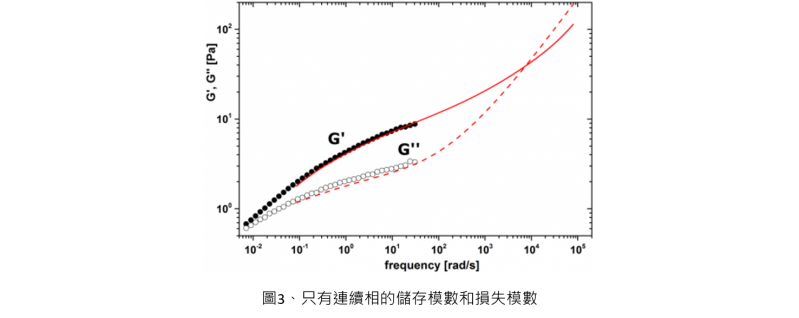
只有連續相的儲存模數（以實心記號，及實線表示）和損失模數（以空心記號，及虛線表示）。紅色「線」表示擴散波光譜法微流變儀的數據，黑色「記號」表示機械式流變儀的數據。

圖三為比較由擴散波光譜法微流變儀與機械式流變儀測得的G'和G''數值，在頻率重疊的範圍，數據顯得相當一致，而且，頻率交叉點（代表G'= G''）位於10⁴ rad/s，與文獻資料一致[4]。

比較圖二及圖三，我們發現乳膠的模數比連續相的模數高約50%，而且整體曲線的形狀非常相似。這證實了分散相佔少量體積百分比的乳膠，其流變學特性主要是由連續相所決定的假設。在近似值假設中（crude approximation），液體微滴在乳膠中，可以理解成像是懸浮固體微粒增加整體黏度η的現象，而其整體黏度與連續相黏度η0的比值，根據巴奇勒方程式（Batchelor equation）[5]，呈現如下︰

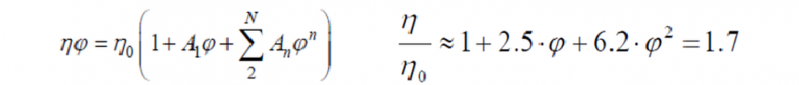
其中η代表整體的黏度，代表η0代表連續相的黏度，φ代表分散相的體積分率，當η/η0=1時，φ=0，當體積分率φ=0.2時，帶入公式可以得到η=1.7η0，也就是說整體黏度是連續相黏度的1.7倍，由模數與黏度的關係式得到，乳膠的模數=G"(ω)=ηω=1. 7〔η0ω〕中，代表理論上乳膠的模數應該比連續相模數多70%，但是，實際上觀察到的值卻只有多50%，這或許可以解釋成因為微滴具有多分散性（polydispersity）的原因，所以整體乳膠的模數只比連續相的模數多50%而非理論值的70%。

結論

我們將擴散波光譜微流變技術應用含油的乳膠水溶液（oil-in-water emulsion）上，並且將結果和機械式流變儀做比較，在重疊的頻率範圍，可以發現這兩個技術之間有非常好的一致性，而且，分別用擴散波光譜法微流變學儀與機械式流變儀進行黃原膠連續相的特性分析，可以發現非常好的一致性，同時也跟文獻資料一致。這表示微滴，也就是分散相，可以充當探測乳膠流變特性的示蹤粒子，而且，當微滴尺寸大小已知的時候，我們發現，擴散波光譜微流變技術非常適合用於乳膠特性的定量。

然而，必須注意的是，當微滴的尺寸大小在連續相的乳膠中是不均勻的情況下，定量乳膠的特性是非常困難的，因為作為探針的微滴在每一個局部的環境都是不同的[6]，但是，這並不是我們所要研究的系統模型，因為在我們選的濃度中，黃原膠所構成的網狀結構大約是40nm的篩孔大小[4]，此大小遠低於微滴尺寸。

最後，由擴散波光譜法微流變儀所得到的數值，具有很高的再現性，因而在與時間有關的特性研究上，例如乳膠的老化及穩定特性等，是非常有價值的工具。

參考文獻

• D.A. Weitz, and D.J. Pine, Diffusion Wave Spectroscopy. In Dynamic Light Scattering; Brown,W., Ed.; Oxford University Press: New York, 652-720 (1993)
• D. Lopez-Diaz, and R. Castillo, Microrheology of solutions embedded with thread-like supramolecularstructures, Soft Matter 7, 5926–5937 (2011)
• E. Choppe, F. Puaud, T. Nicolai, and L. Benyahia, Rheology of xanthan solutions as a function of temperature, concentration and ionic strength, Carbohydrate Polymers 82 (2010)
• K.v Gruijthuijsen, H. Vishweshwara, R. Tuinier, P. Schurtenberger, and A. Stradner, Origin of suppressed demixing in casein/xanthan-mixtures, Soft Matter 8 (2011)
• S.R. Derkach, Rheology on the way from dilute to concentrated emulsions, Inter. Rev. Chem. Eng. 2 (2009)
• F.K. Oppong, L. Rubatat, B.J. Frisken, A.E. Bailey and J.R. de Bruyn, Microrheology and structure of a yield-stress polymer gel, Physical Review E 73 (2006)
• Emulsions Characterization

關鍵字詞

• DWS, Diffusing Wave Spectroscopy︰擴散波光譜法
• Monodisperse︰單分散性
• Polydispersity︰多分散性
• Liquid droplets︰液體微滴
• Homogenization︰均質化
• Aging︰老化
• Transmission mode︰前向散射模式
• l*, Transport mean free path︰運輸平均自由徑
• Continuous phase︰連續相
• Disperse phase︰分散相
• Batchelor equation︰巴奇勒方程式